Childs-Kothari-Somma (CKS)#

CKS(A, b, eps, kappa=None, max_beta=None)[source]#

Performs the Childs–Kothari–Somma (CKS) quantum algorithm to solve the Quantum Linear Systems Problem (QLSP) \(A \vec{x} = \vec{b}\), using the Chebyshev approximation of \(1/x\).

The algorithm prepares a quantum state \(\ket{x} \propto A^{-1} \ket{b}\) within target precision \(\epsilon\) of the ideal solution \(\ket{x}\).

The asymptotic complexity is \(\mathcal{O}\!\left(\log(N)s \kappa^2 \text{polylog}\!\frac{s\kappa}{\epsilon}\right)\), where \(N\) is the matrix size, \(s\) its sparsity, and \(\kappa\) its condition number. This represents an exponentially better precision scaling compared to the HHL algorithm.

This function integrates all core components of the CKS approach: Chebyshev polynomial approximation, linear combination of unitaries (LCU), qubitization with reflection operators, and the Repeat-Until-Success (RUS) protocol. The semantics of the approach can be illustrated with the following circuit schematics:

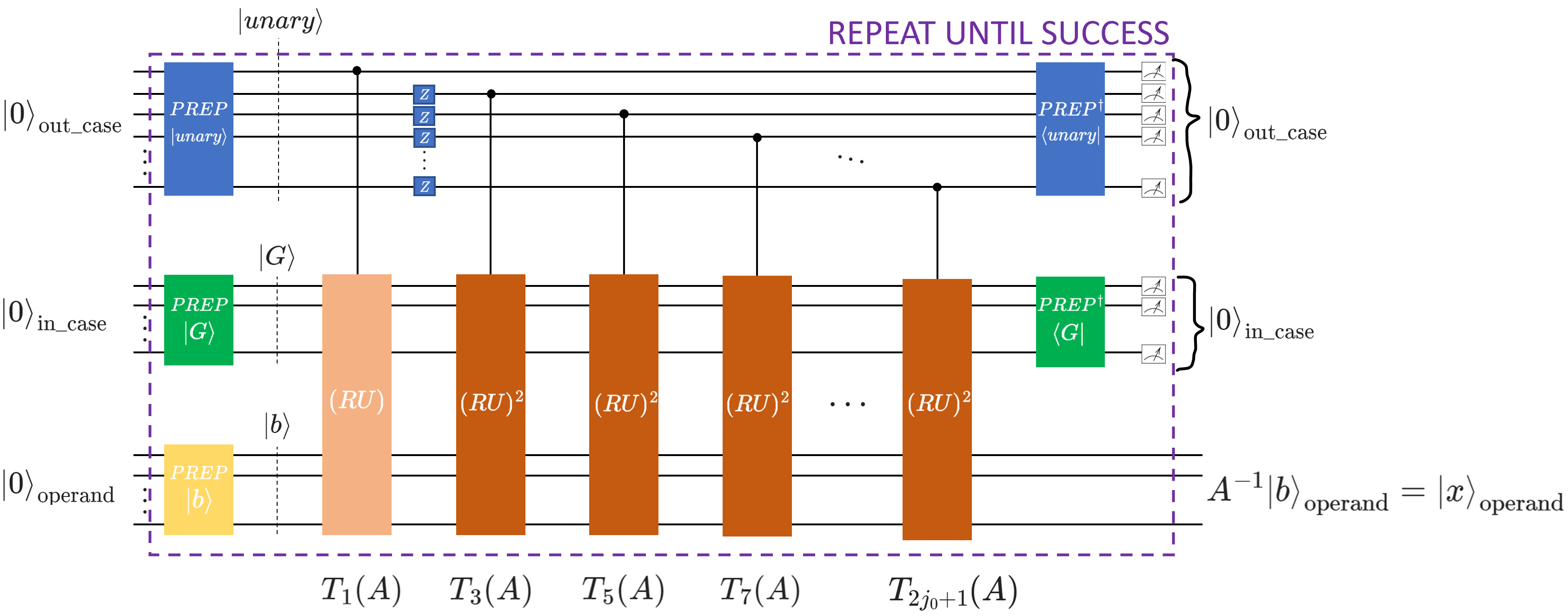
../../_images/CKS_schematics.png
Implementation overview:

  1. Compute the CKS parameters \(j_0\) and \(\beta\) (CKS_parameters()).

  2. Generate Chebyshev coefficients and the auxiliary unary state (cheb_coefficients(), unary_prep()).

  3. Build the core LCU structure and qubitization operator (inner_CKS()).

  4. Apply the RUS post-selection step to project onto the valid success outcome.

This function supports interchangeable and independent input types for both the matrix A and vector b from the QLSP \(A\vec{x} = \vec{b}\).

Case distinctions for A

  • Matrix input:

    A is either a NumPy array (Hermitian matrix), or SciPy Compressed Sparse Row matrix (Hermitian matrix). The block encoding unitary \(SEL\) and state preparation unitary \(PREP\) are constructed internally from A via Pauli decomposition.

  • Block-encoding input:

    A is a 3-tuple (U, state_prep, n) representing a block-encoding:

    • Ucallable

      Callable U(operand, case) applies the block-encoding unitary \(SEL\).

    • state_prepcallable

      Callable state_prep(case) applies the block-encoding state preparatiion unitary \(PREP\) to an auxiliary case QuantumVariable .

    • nint

      The size of the auxiliary case QuantumVariable.

    In this case, (an upper bound for) the condition number kappa must be specified. Additionally, the block-encoding unitary \(U\) supplied must satisfy the property \(U^2 = I\), i.e., it is self-inverse. This condition is required for the correctness of the Chebyshev polynomial block encoding and qubitization step. Further details can be found here.

Case distinctions for b

  • Vector input:

    If b is a NumPy array, a new operand QuantumFloat is constructed, and state preparation is performed via prepare(operand, b).

  • Callable input:

    If b is a callable, it is assumed to prepare the operand state when called. The operand QuantumFloat is generated directly via operand = b().

Parameters:
Anumpy.ndarray or scipy.sparse.csr_matrix or tuple

Either the Hermitian matrix \(A\) of size \(N \times N\) from the linear system \(A \vec{x} = \vec{b}\), or a 3-tuple (U, state_prep, n) representing a preconstructed block-encoding.

bnumpy.ndarray or callable

Either a vector \(\vec{b}\) of the linear system, or a callable that prepares the corresponding quantum state operand.

epsfloat

Target precision \(\epsilon\), such that the prepared state \(\ket{\tilde{x}}\) is within error \(\epsilon\) of \(\ket{x}\).

kappafloat, optional

Condition number \(\kappa\) of \(A\). Required when A is a block-encoding tuple (U, state_prep, n) rather than a matrix.

max_betafloat, optional

Optional upper bound on the complexity parameter \(\beta\).

Returns:
operandQuantumVariable

Quantum variable containing the final (approximate) solution state \(\ket{\tilde{x}} \propto A^{-1}\ket{b}\). When the internal RUS decorator reports success (success_bool = True), this variable contains the valid post-selected solution. If success_bool is False, the simulation automatically repeats until success.

Examples

The following examples demonstrate how the CKS algorithm can be applied to solve the quantum linear systems problem (QLSP) \(A \vec{x} = \vec{b}\), using either a direct Hermitian matrix input or a preconstructed block-encoding representation.

Example 1: Solving a 4×4 Hermitian system

First, we define a small Hermitian matrix \(A\) and a right-hand side vector \(\vec{b}\):

import numpy as np

A = np.array([[0.73255474, 0.14516978, -0.14510851, -0.0391581],
              [0.14516978, 0.68701415, -0.04929867, -0.00999921],
              [-0.14510851, -0.04929867, 0.76587818, -0.03420339],
              [-0.0391581, -0.00999921, -0.03420339, 0.58862043]])

b = np.array([0, 1, 1, 1])

Next, we solve this linear system using the CKS quantum algorithm:

from qrisp.algorithms.cks import CKS
from qrisp.jasp import terminal_sampling

@terminal_sampling
def main():

    x = CKS(A, b, 0.01)
    return x

res_dict = main()

The resulting dictionary contains the measurement probabilities for each computational basis state. To extract the corresponding quantum amplitudes (up to sign):

for k, v in res_dict.items():
    res_dict[k] = v**0.5

q = np.array([res_dict.get(key, 0) for key in range(len(b))])
print("QUANTUM SIMULATION\n", q)
# QUANTUM SIMULATION
# [0.02714082 0.55709921 0.53035395 0.63845794]

We compare this to the classical normalized solution:

c = (np.linalg.inv(A) @ b) / np.linalg.norm(np.linalg.inv(A) @ b)

print("CLASSICAL SOLUTION\n", c)  
# CLASSICAL SOLUTION
# [0.02944539 0.55423278 0.53013239 0.64102936]

We see that we obtained the same result in our quantum simulation up to precision \(\epsilon\)!

To perform quantum resource estimation, replace the @terminal_sampling decorator with @count_ops(meas_behavior="0"):

from qrisp.jasp import count_ops

@count_ops(meas_behavior="0")
def main():

    x = CKS(A, b, 0.01)
    return x

res_dict = main()
print(res_dict)
# {'cx': 3628, 't': 1288, 't_dg': 1702, 'p': 178, 'cz': 138, 'cy': 46, 'h': 960, 'x': 324, 's': 66, 's_dg': 66, 'u3': 723, 'gphase': 49, 'ry': 2, 'z': 11, 'measure': 16}

The printed dictionary lists the estimated quantum gate counts required for the CKS algorithm. Since the simulation itself is not executed, this approach enables scalable gate count estimation for linear systems of arbitrary size.

Example 2: Using a custom block encoding

The previous example displays how to solve the linear system for any Hermitian matrix \(A\), where the block-encoding is constructed from the Pauli decomposition of \(A\). While this approach is efficient when \(A\) corresponds to, e.g., an Ising or a Heisenberg Hamiltonian, the number of Pauli terms may not scale favorably in general. For certain sparse matrices, their structure can be exploited to construct more efficient block-encodings.

In this example, we construct a block-encoding representation for the following tridiagonal sparse matrix:

import numpy as np

def tridiagonal_shifted(n, mu=1.0, dtype=float):
    I = np.eye(n, dtype=dtype)
    return (2 + mu) * I - 2*np.eye(n, k=n//2, dtype=dtype) - 2*np.eye(n, k=-n//2, dtype=dtype)

N = 8
A = tridiagonal_shifted(N, mu=3)
b = np.random.randint(0, 2, size=N)

print(A)
# [[ 5.  0.  0.  0. -2.  0.  0.  0.]
#  [ 0.  5.  0.  0.  0. -2.  0.  0.]
#  [ 0.  0.  5.  0.  0.  0. -2.  0.]
#  [ 0.  0.  0.  5.  0.  0.  0. -2.]
#  [-2.  0.  0.  0.  5.  0.  0.  0.]
#  [ 0. -2.  0.  0.  0.  5.  0.  0.]
#  [ 0.  0. -2.  0.  0.  0.  5.  0.]
#  [ 0.  0.  0. -2.  0.  0.  0.  5.]]

This matrix can be decomposed using three unitaries: the identity \(I\), and two shift operators \(V\colon\ket{k}\rightarrow-\ket{k+N/2 \mod N}\) and \(V^{\dagger}\colon\ket{k}\rightarrow-\ket{k-N/2 \mod N}\). We define their corresponding functions:

from qrisp import gphase, prepare, qswitch

def I(qv):
    pass

def V(qv):
    qv += N//2
    gphase(np.pi, qv[0])

def V_dg(qv):
    qv -= N//2
    gphase(np.pi, qv[0])

unitaries = [I, V, V_dg]

Additionally, the block encoding unitary \(U\) supplied must satisfy the property \(U^2 = I\), i.e., it is self-inverse. This condition is required for the correctness of the Chebyshev polynomial block encoding and qubitization step. Further details can be found here. In this case, the fact that \(V^2=(V^{\dagger})^2=I\) ensures that defining the block encoding unitary via a quantum switch case satsifies \(U^2 = I\).

We now define the block_encoding (U, state_prep, n):

coeffs = np.array([5,1,1])
alpha = np.sum(coeffs)

def U(case, operand):
    qswitch(operand, case, unitaries)

def state_prep(case):
    prepare(case, np.sqrt(coeffs/alpha))

block_encoding = (U, state_prep, 2)

We solve the linear system by passing this block-encoding tuple as A into the CKS function:

@terminal_sampling
def main():

    x = CKS(block_encoding, b, 0.01, np.linalg.cond(A))
    return x

res_dict = main()

We, again, compare the solution obtained by quantum simulation with the classical solution

for k, v in res_dict.items():
    res_dict[k] = v**0.5

q = np.array([res_dict.get(key, 0) for key in range(N)])
c = (np.linalg.inv(A) @ b) / np.linalg.norm(np.linalg.inv(A) @ b)

print("QUANTUM SIMULATION\n", q, "\nCLASSICAL SOLUTION\n", c)
# QUANTUM SIMULATION
# [0.43917486 0.31395935 0.12522139 0.43917505 0.43917459 0.12522104 0.31395943 0.43917502]
# CLASSICAL SOLUTION
# [0.43921906 0.3137279  0.12549116 0.43921906 0.43921906 0.12549116 0.3137279  0.43921906]

Quantum resource estimation can be performed in the same way as in the first example:

@count_ops(meas_behavior="0")
def main():

    x = CKS(block_encoding, b, 0.01, np.linalg.cond(A))
    return x

res_dict = main()
print(res_dict)
# {'h': 676, 't_dg': 806, 'cx': 1984, 't': 651, 's': 152, 's_dg': 90, 'u3': 199, 'gphase': 65, 'p': 149, 'z': 15, 'x': 126, 'measure': 142, 'ry': 2}

Finally, note that it is also possible to solve a linear system without using the Repeat-Until-Success decorator, by performing the necessary post-selection manually. Such an example can be found in inner_CKS().

Circuit construction#

inner_CKS(A, b, eps[, kappa, max_beta])

Miscellaneous#

CKS_parameters(A, eps[, kappa, max_beta])

Computes the Chebyshev-series complexity parameter \(\beta\) and the truncation order \(j_0\) for the truncated Chebyshev approximation of \(1/x\) used in the Childs–Kothari–Somma quantum algorithm.

cheb_coefficients(j0, b)

Calculates the positive coefficients \(\alpha_i\) for the truncated Chebyshev expansion of \(1/x\) up to order \(2j_0+1\), as described in the Childs–Kothari–Somma paper.

unary_prep(case, coeffs)

Prepares the unary-encoded state \(\ket{\text{unary}}\) of Chebyshev coefficients.
On this page

Get in touch!

If you are interested in Qrisp or high-level quantum algorithm research in general connect with us on our Slack workspace.

Enable interactive documentation via Thebe.